luas segi-n beraturan, jari jari lingkarang luar dan lingkaran dalam segitiga, garis singgung persekutuan luar/dalam lingkaran
Luas dan Keliling Bangun Datar Segi-n Beraturan
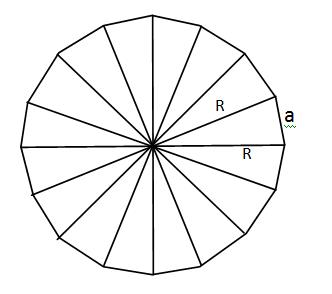
Pada dasarnya bangun datar segi-n beraturan terbentuk dari lingkaran yang dibagi-bagi menjadi beberapa bagian yang sama besar (berbentuk segitiga sama kaki). Sehingga untuk menghitung luas dan keliling bangun datar segi-n kita akan melibatkan sudut pusat dan jari-jarinya. Sudut pusatnya adalah sudut pada segitiga dengan besarnya adalah yang ditunjukkan oleh tanda sudut warna merah. Sementara sisi dari bangun datar segi-n ditunjukkan oleh huruf . Perhatikan gambar berikut ini.
Dalam menghitung Luas dan Keliling Bangun Datar Segi-n Beraturan, kita melibatkan rumus luas segitiga yang melibatkan sudut yaitu lebih tepatnya luas segitiga menggunakan sinus dan untuk menghitung kelilingnya kita menggunakan konsep aturan kosinus. Silahkan teman-teman baca materinya pada artikel : "Penerapan Trigonometri pada Segitiga : Aturan Sinus, Aturan Cosinus, Luas Segitiga". Untuk lebih memudahkan, teman-teman sebaiknya juga mempelajari nilai perbandingan fungsi trigonometri pada sudut-sudut istimewa pada artikel "Perbandingan Trigonometri Sudut-sudut Berelasi".
*). Luas segitiga menggunaan sinus.
Perhatikan segitga PRQ pada segienam di atas (sebagai contoh saja), luasnya adalah :
Luas segitiga .
*). Luas bangun datar segi-n beraturan :
Luas segi-n luas segitiga
Luas segi-n
Keliling bangun datar segi-n beraturan :
*). Aturan kosinus menentukan pajang sisi segin-n ().
Berdasarkan aturan kosinus pada segitiga PRQ, panjang adalah
*). Keliling bangun datar segi-n beraturan
Keliling .
keterangan :
sudut pusat .
Contoh soal Luas dan Keliling Bangun Datar Segi-n Beraturan :
1). Pada segienam beraturan dengan jari-jari 10 cm, tentukan :
a). Luas,
b). Keliling.
Penyelesaian :
*). Pada soal diketahui .
Bangun datar segienam artinya .
a). Luas segienam beraturan:
Jadi, luas segienam tersebut adalah .
b). Keliling segienam beraturan,
Jadi, keliling segienam tersebut adalah .
2). Sebuah bangun datar segi-8 beraturan memiliki keliling cm. Tentukan
a). Panjang sisi dan jari-jarinya,
b). Tentukan luas segidelapan tersebut.
Penyelesaian :
a). Panjang sisi dan jari-jari :
*). Panjang sisi,
Sehingga panjang sisinya adalah cm.
*). Jari-jari :
Sehingga panjang jari-jarinya .
b). Luas segidelapan beraturan :
Jadi, luas segidelapan tersebut adalah .
3). Luas bangun datar segi-12 beraturan adalah 27 cm. Tentukan :
a). Panjang jari-jari dan panjang sisi,
b). Keliling segi-12 tersebut.
Penyelesaian :
a). Panjang jari-jari dan panjang sisi,
*). Panjang jari-jari :
Sehingga cm.
*). Panjang sisi segi-12 :
Sehingga panjang sisi
b). Keliling segi-12 tersebut.
Keliling
Jadi, keliling segi-12 adalah .
4). Sebuah bangun datar segienam beraturan memeiliki jari-jari cm, tentukan :
a). Luas,
b). Keliling.
Penyelesaian :
*). Pada soal diketahui jari-jari .
Bangun datar segienam artinya .
a). Luas segienam beraturan:
Jadi, luas segienam tersebut adalah .
b). Keliling segienam beraturan,
Jadi, keliling segienam tersebut adalah .
Demikian pembahasan materi Luas dan Keliling Bangun Datar Segi-n Beraturan dan contoh-contohnya. Silahkan juga baca materi lain yang berkaitan dengan Luasan.
Luas Segi n Beraturan
Pada segi n beraturan
Setiap segi n beraturan bisa kita bagi menjadi n buah segitiga yang kongruen
Setiap titik sudut pada segi n beraturan bisa dilalui sebuah lingkaran, lingkaran ini disebut lingkaran luar segi n. Semuat titik sudut akan dilewati lingkaran (tidak ada yang tertinggal).
Menghitung luas segi n beraturan akan lebih mudah jika diketahui jari-jari lingkaran luarnya
Setiap segi n bisa dibagi menjadi n buah segitiga yang kongruen seperti pada gambar di atas.
Selanjutnya kita ambil salah satu segitiganya
Besar sudut A adalah 
Luas segitiga adalah
LΔ = ½ .R.R sin A

Luas segi n beraturan adalah
Ln = n. LΔ

Rumus ini merupakan rumus luas segi n beraturan yang diketahui jari-jari lingkaran luarnya.
Bagaimana jika diketahui sisinya ?
Pertama kita cari dulu hubungan antara jari-jari lingkaran luar (R) dengan sisinya (a)
Dengan aturan cosinus maka
a2 = R2 + R2 — 2R.R cos A
a2 = 2R2 — 2R2 cos A
a2 = R2(2 — 2cos A)

Luas segi n :
Jadi luas segi n beraturan yang panjang sisinya a adalah



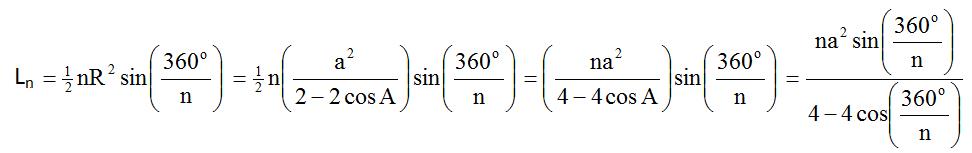
Komentar
Posting Komentar