SOAL DAN PEMBAHASAN FUNGSI TRIGOMETRI

 

Soal dan Pembahasan – Fungsi Trigonometri dan Grafiknya

Soal Nomor 1
Diketahui grafik fungsi $y_1=5\sin x$ dan $y_2=\sin 5x$. Pernyataan berikut yang benar adalah $\cdots \cdot$
A. periode $y_1$ = periode $y_2$
B. amplitudo $y_1$ = amplitudo $y_2$
C. periode $y_1=\frac{1}{5}$ kali periode $y_2$
D. amplitudo $y_1=\frac{1}{5}$ kali amplitudo $y_2$
E. amplitudo $y_1=5$ kali amplitudo $y_2$

Pembahasan

Bentuk umum fungsi sinus tersebut adalah $y=a\sin kx$.
Periode:
Periode $y_1=5\sin x$ dengan $k=1$ adalah $P_1=\frac{{360}^{\circ }}{1}={360}^{\circ }$, sedangkan periode $y_2=\sin 5x$ dengan $k=5$ adalah $P_2=\frac{{360}^{\circ }}{5}={72}^{\circ }$.
Dapat disimpulkan bahwa periode $y_1$ sama dengan 5 kali periode $y_2$.
Amplitudo:
Amplitudo $y_1=5\sin x$ dengan $a=5$ adalah $A_1=|a|=|5|=5$, sedangkan amplitudo $y_2=\sin 5x$ dengan $a=1$ adalah $A_2=|a|=|1|=1$. Dapat disimpulkan bahwa amplitudo $y_1$ 5 kali amplitudo $y_2$.
Pernyataan yang benar ada pada pilihan E.

Soal Nomor 2
Grafik $f\left(x\right)=2\cos x$ memotong sumbu-$X$ di titik berkoordinat $\cdots \cdot$
A. $({30}^{\circ },0)$              D. $({90}^{\circ },0)$
B. $({45}^{\circ },0)$              E. $({180}^{\circ },0)$
C. $({60}^{\circ },0)$

Pembahasan

Apabila grafik memotong sumbu-$X$, maka nilai $f\left(x\right)=y=0$. Dengan demikian,
$f\left(x\right)=2\cos x\Rightarrow 0=2\cos x\iff \cos x=0$
Nilai $x$ yang membuat $\cos x$ bernilai 0 adalah ${90}^{\circ }$.
Jadi, titik potong grafiknya berkoordinat $({90}^{\circ },0)$
(Jawaban D)

[collapse]

Soal Nomor 3
Grafik di atas adalah grafik fungsi $\cdots \cdot$

A. $f\left(x\right)=\frac{1}{2}\sin \frac{1}{2}x$
B. $f\left(x\right)=\frac{1}{2}\sin 2x$
C. $f\left(x\right)=\frac{1}{2}\cos 2x$
D. $f\left(x\right)=2\cos \frac{1}{2}x$
E. $f\left(x\right)=2\cos 2x$

Pembahasan

Perhatikan sketsa gambar berikut.

Grafik di atas merupakan modifikasi grafik cosinus (karena grafiknya dimulai dari sumbu-$Y$) dengan bentuk umum $f\left(x\right)=a\cos kx$.
Grafik juga menunjukkan bahwa nilai maksimum fungsinya $\frac{1}{2}$, sedangkan nilai minimumnya $-\frac{1}{2}$, sehingga
$\begin{array}{cc}a& =\frac{\text{N. Maksimum}-\text{N. Minimum}}{2}\\ & =\frac{\frac{1}{2}-(-\frac{1}{2})}{2}=\frac{1}{2}\end{array}$
Saat $x=0^{\circ }$, nilai fungsinya $\frac{1}{2}$, lalu berulang kembali di $x=\pi$, sehingga periodenya $\pi$. Dengan demikian, $k=\frac{2\pi }{\text{Periode}}=\frac{2\pi }{\pi }=2$.
Jadi, grafik fungsi di atas adalah grafik fungsi $f\left(x\right)=\frac{1}{2}\cos 2x$
(Jawaban C)

[collapse]

Soal Nomor 4
Grafik di atas adalah grafik fungsi $\cdots \cdot$

A. $y=2\sin x,0^{\circ }\le x\le {270}^{\circ }$
B. $y=2\cos 4x,0^{\circ }\le x\le {270}^{\circ }$
C. $y=4\sin 2x,0^{\circ }\le x\le {270}^{\circ }$
D. $y=4\cos 2x,0^{\circ }\le x\le {270}^{\circ }$
E. $y=4\sin 4x,0^{\circ }\le x\le {270}^{\circ }$

Pembahasan

Perhatikan sketsa gambar berikut.

Beranjak dari grafik sinus yang memiliki bentuk umum $f\left(x\right)=a\sin kx$, kurva pada gambar tidak bergeser dan berawal dari titik $(0,0)$. Grafik juga menunjukkan bahwa nilai maksimum dan minimum fungsi adalah $4$ dan $-4$, sehingga
$\begin{array}{cc}a& =\frac{\text{N. Maksimum}-\text{N. Minimum}}{2}\\ & =\frac{4-(-4)}{2}=4\end{array}$
Pada saat nilai $x={180}^{\circ }$, fungsi kembali bernilai $0$, lalu berulang kembali seperti sebelumnya, sehingga periodenya adalah ${180}^{\circ }$, dan akibatnya
$k=\frac{{360}^{\circ }}{{180}^{\circ }}=2$
Jadi, rumus fungsi $f\left(x\right)=4\sin 2x$ dengan batas interval $0^{\circ }\le x\le {270}^{\circ }$
(Jawaban C)

[collapse]

Soal Nomor 5
Grafik fungsi $f\left(x\right)=-2\cos 3x,-\pi \le x\le \pi$adalah $\cdots \cdot$

Pembahasan

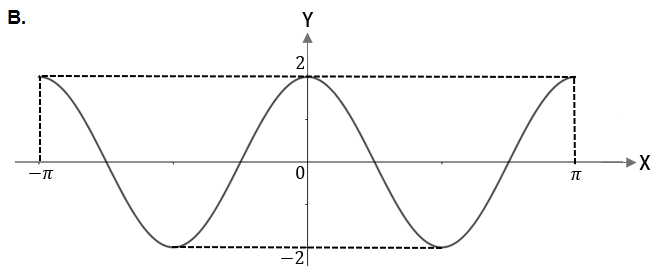
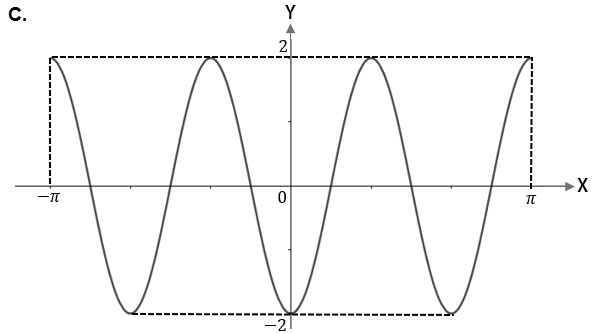
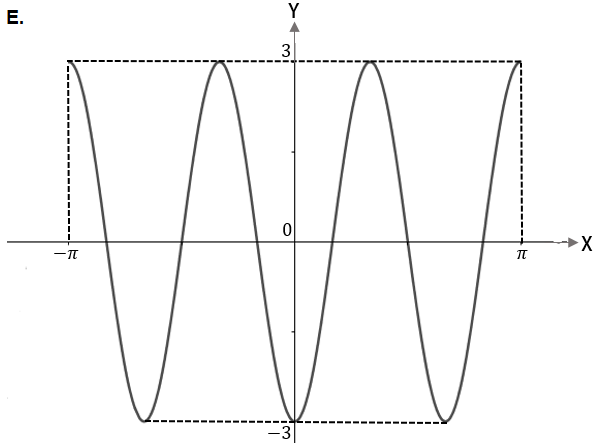
Bentuk umum fungsi cosinus adalah $f\left(x\right)=a\cos kx$. Oleh karena $f\left(x\right)=-2\cos 3x$, maka $a=-2$ dan $k=3$.
Amplitudo grafiknya adalah $-(-a)=a=2$dan saat $x=0^{\circ }$, nilai fungsinya adalah $f\left(0\right)=-2\cos 3\left(0\right)=-2\left(1\right)=-2$,
sehingga pilihan B, D, E tereliminasi.
Karena $k=3$, maka periode fungsinya adalah 
$\begin{array}{cc}k& =\frac{2\pi }{\text{Periode}}\\ 3& =\frac{2\pi }{\text{Periode}}\iff \text{Periode}=\frac{2}{3}\pi \end{array}$
Pada pilihan A, periode grafiknya adalah $\pi -(-\pi )=2\pi$, sedangkan pada pilihan C, periode grafiknya dapat dilihat dengan observasi berikut: dari titik $x=0$ ke titik $x=\pi$ terdapat 1,5 gelombang (1,5 lembah; 1,5 bukit), sehingga periodenya adalah $\frac{\pi -0}{1,5}=\frac{2}{3}\pi$
Jadi, grafik fungsi $f\left(x\right)=-2\cos 3x$ditunjukkan pada pilihan C. 

[collapse]

Soal Nomor 6
Fungsi yang sesuai dengan grafik berikut adalah $\cdots \cdot$

A. $f\left(x\right)=2\sin (x-\frac{\pi }{2})$
B. $f\left(x\right)=\sin (2x+\frac{\pi }{2})$
C. $f\left(x\right)=2\sin (x+\frac{\pi }{2})$
D. $f\left(x\right)=\sin (2x-\frac{\pi }{2})$
E. $f\left(x\right)=2\sin (2x+\frac{\pi }{2})$

Pembahasan

Beranjak dari grafik sinus: karena kurva bergeser (ke kiri) sejauh $\frac{\pi }{2}$, maka bentuk umum grafik fungsinya adalah $f\left(x\right)=y=a\sin k(x-c)$.
Untuk grafik ini, nilai $c$ yang menentukan pergeseran kurva adalah $-\frac{\pi }{2}$ (tandanya negatif, karena grafik bergeser ke kiri).
Dimulai dari titik $x=-\frac{\pi }{2}$ yang nilai fungsinya 0, grafik fungsi kembali bernilai $0$dan berulang kembali di titik $x=\frac{3\pi }{2}$, sehingga periode grafik fungsinya adalah $\frac{3\pi }{2}–(-\frac{\pi }{2})=2\pi$.
Dengan demikian,
$k=\frac{2\pi }{\text{Periode}}=\frac{2\pi }{2\pi }=1$
Nilai $a$ ditentukan oleh nilai maksimum dan nilai minimum fungsi, yakni
$\begin{array}{cc}a& =\frac{\text{N. Maksimum}-\text{N. Minimum}}{2}\\ & =\frac{2-(-2)}{2}=2\end{array}$
Jadi, rumus grafik fungsinya adalah $f\left(x\right)=2\sin 1(x+\frac{\pi }{2})=2\sin (x+\frac{\pi }{2})$
(Jawaban C)

[collapse]

Soal Nomor 7
Perhatikan grafik berikut.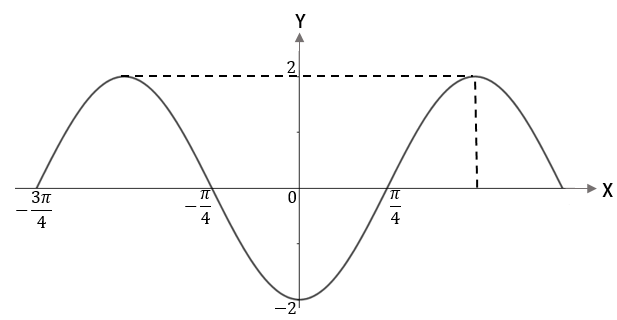

Fungsi yang memenuhi grafik di atas adalah $\cdots \cdot$
A. $f\left(x\right)=-2\sin (x-\frac{\pi }{4})$
B. $f\left(x\right)=-2\sin (x+\frac{\pi }{4})$
C. $f\left(x\right)=-2\sin (2x-\frac{\pi }{2})$
D. $f\left(x\right)=-2\sin (2x+\frac{\pi }{2})$
E. $f\left(x\right)=-2\sin (2x-\frac{\pi }{4})$

Pembahasan

Beranjak dari grafik sinus: karena kurva bergeser (ke kiri) sejauh $\frac{\pi }{4}$, maka bentuk umum grafik fungsinya adalah $f\left(x\right)=y=a\sin k(x-c)$.
Untuk grafik ini, nilai $c$ yang menentukan pergeseran kurva adalah $-\frac{\pi }{4}$.
Dimulai dari titik $x=-\frac{3\pi }{4}$ yang nilai fungsinya 0, grafik fungsi kembali bernilai $0$dan berulang kembali di titik $x=\frac{\pi }{4}$, sehingga periode grafik fungsinya adalah $\frac{\pi }{4}–(-\frac{3\pi }{4})=\pi$.
Dengan demikian,
$k=\frac{2\pi }{\text{Periode}}=\frac{2\pi }{\pi }=2$
Nilai $a$ ditentukan oleh nilai maksimum dan nilai minimum fungsi, yakni
$\begin{array}{cc}a& =\frac{\text{N. Maksimum}-\text{N. Minimum}}{2}\\ & =\frac{2-(-2)}{2}=2\end{array}$
Catatan: Pilihan ganda pada soal menunjukkan bahwa $a=-2$, artinya kurva sinus menurun, lalu menanjak. Ini menjadi alasan mengapa kita anggap kurva bergeser ke kiri.
Jadi, rumus grafik fungsinya adalah $$f\left(x\right)=-2\sin 2(x+\frac{\pi }{4})=-2\sin (2x+\frac{\pi }{2})$$(Jawaban D)

[collapse]

Soal Nomor 8
Grafik fungsi berikut adalah sketsa grafik dari $y=a\cos kx$. Nilai $a$ dan $k$ berturut-turut adalah $\cdots \cdot$

A. $-2\text{dan}1$                   D. $2\text{dan}1$
B. $-2\text{dan}2$                   E. $2\text{dan}-1$
C. $2\text{dan}2$

Pembahasan

Nilai $a$ ditentukan oleh nilai maksimum dan nilai minimum fungsi, yakni
$\begin{array}{cc}a& =\frac{\text{N. Maksimum}-\text{N. Minimum}}{2}\\ & =\frac{2-(-2)}{2}=2\end{array}$
Grafik menunjukkan bahwa saat $x=0$, nilai fungsinya $-2$, begitu juga saat $x=2\pi$. Ini berarti, periode grafiknya adalah $2\pi$, sehingga dengan menggunakan rumus periode, diperoleh
$2\pi =\frac{2\pi }{k}\iff k=1$
Jadi, $a$ dan $k$ berturut-turut adalah $a=-2$dan $k=1$
(Jawaban A)

[collapse]

Soal Nomor 9
Diketahui $f\left(x\right)=\cos x+3$ dengan $0\le x\le 2\pi$. Daerah hasil fungsi $f\left(x\right)$ adalah $\cdots \cdot$
A. $-3\le f\left(x\right)\le 3$              D. $0\le f\left(x\right)\le 3$
B. $-2\le f\left(x\right)\le 2$              E. $2\le f\left(x\right)\le 4$
C. $-1\le f\left(x\right)\le 1$

Pembahasan

Agar $f\left(x\right)=\cos x+3$ mencapai maksimum, maka $\cos x$ haruslah sebesar-besarnya, yaitu $\cos x=1$. Untuk itu,
$f_{\text{maks}}\left(x\right)=1+3=4$
Agar $f\left(x\right)=\cos x+3$ mencapai minimum, maka $\cos x$ haruslah sekecil-kecilnya, yaitu $\cos x=-1$. Untuk itu,
$f_{\text{min}}\left(x\right)=-1+3=2$
Jadi, daerah hasil fungsi $f\left(x\right)$ adalah semua nilai (bilangan real) dari $2$ sampai $4$, atau secara matematis ditulis $2\le f\left(x\right)\le 4$
(Jawaban E)

[collapse]

Soal Nomor 10
Nilai minimum $f\left(x\right)=2\sin (x–\frac{\pi }{3})+1$ adalah $\cdots \cdot$
A. $-3$                      C. $-1$                   E. $3$
B. $-2$                      D. $1$            

Pembahasan

Nilai minimum $f\left(x\right)=2\sin (x–\frac{\pi }{3})+1$tercapai ketika $\sin (x-\frac{\pi }{3})$ bernilai sekecil-kecilnya, yaitu $\sin (x-\frac{\pi }{3})=-1$. Untuk itu,
$f_{\text{min}}\left(x\right)=2(-1)+1=-1$
Jadi, nilai minimum $f\left(x\right)$ adalah $-1$
(Jawaban C)

[collapse]

Soal Nomor 11
Fungsi $f\left(x\right)=2–5\sin \frac{\pi x}{6}$ untuk $-5\le x\le 1$mempunyai nilai maksimum $p$ di titik $x=q$. Nilai $p+q=\cdots \cdot$
A. $7$                      C. $5$                     E. $3$
B. $6$                      D. $4$           

Pembahasan

Agar $f\left(x\right)=2–5\sin \frac{\pi x}{6}$ , nilai $\sin \frac{\pi x}{6}$haruslah sekecil mungkin (negatif). Karena nilai minimum sinus adalah $-1$, maka dalam hal ini
$\begin{array}{cc}\sin \frac{\pi x}{6}& =-1\\ \sin \frac{\pi x}{6}& =\sin \frac{3\pi }{2}\\ \frac{\pi x}{6}& =\frac{3\pi }{2}\\ \pi x& =9\pi \\ x& =9\end{array}$
Nilai $x$ yang diperoleh berada di luar interval sehingga tidak memenuhi.
Di kasus lain,
$\begin{array}{cc}\sin \frac{\pi x}{6}& =-1\\ \sin \frac{\pi x}{6}& =-\sin \frac{\pi }{2}\\ \frac{\pi x}{6}& =-\frac{\pi }{2}\\ \pi x& =-3\pi \\ x& =-3\end{array}$
Nilai $x=-3=q$ ini memenuhi interval yang diberikan. Ini berarti, nilai maksimum $f\left(x\right)$adalah
$\begin{array}{cc}f(-3)& =2-5\sin \frac{\pi (-3)}{6}\\ & =2-5(-1)=7\end{array}$
Jadi, nilai $p+q=7+(-3)=4$
(Jawaban D)

[collapse]

Soal Nomor 12
Diketahui $f\left(x\right)=\sqrt{2}\cos 3x+1$. Jika nilai maksimum dan minimum $f\left(x\right)$ berturut-turut adalah $p$ dan $q$, maka nilai $p^2+q^2$ adalah $\cdots \cdot$
A. $1$                     C. $3$                     E. $6$
B. $2$                     D. $4$           

Pembahasan

Nilai maksimum $f\left(x\right)=\sqrt{2}\cos 3x+1$tercapai ketika $\cos 3x$ bernilai sebesar-besarnya, yaitu $\cos 3x=1$. Untuk itu,
$f_{\text{maks}}\left(x\right)=p=\sqrt{2}\left(1\right)+1=\sqrt{2}+1$
Nilai minimum $f\left(x\right)=\sqrt{2}\cos 3x+1$tercapai ketika $\cos 3x$ bernilai sekecil-kecilnya, yaitu $\cos 3x=-1$. Untuk itu,
$f_{\text{min}}(x{)}_{=}q=\sqrt{2}(-1)+1=-\sqrt{2}+1$
Dengan demikian,
$\begin{array}{cc}{p}^2+q^2& =(\sqrt{2}+1{)}^2+(-\sqrt{2}+1{)}^2\\ & =(2+2\sqrt{2}+1)+(2–2\sqrt{2}+1)\\ & =6\end{array}$
Jadi, nilai dari $p^2+q^2=6$
(Jawaban E)

[collapse]

Soal Nomor 13
Nilai $x$ yang memenuhi saat fungsi $f\left(x\right)=-4\sin 3x+2$ memotong sumbu-$X$pada interval ${270}^{\circ }\le x\le {360}^{\circ }$ adalah $\cdots \cdot$
A. ${270}^{\circ }$                      D. ${305}^{\circ }$
B. ${280}^{\circ }$                      E. ${315}^{\circ }$
C. ${290}^{\circ }$

Pembahasan

Ketika kurva memotong sumbu-$X$, ordinatnya akan bernilai $0$ atau $f\left(x\right)=y=0$. Untuk itu, kita peroleh
$\begin{array}{cc}f\left(x\right)& =-4\sin 3x+2\\ \Rightarrow 0& =-4\sin 3x+2\\ -2& =-4\sin 3x\\ \sin 3x& =\frac{-2}{-4}=\frac{1}{2}\\ \sin 3x& =\sin {30}^{\circ }\end{array}$
Perhatikan bahwa interval $x$ adalah ${270}^{\circ }\le x\le {360}^{\circ }$.
Berdasarkan rumus persamaan dasar trigonometri, diperoleh:
Kemungkinan 1
$\begin{array}{cc}3x& ={30}^{\circ }+k\cdot {360}^{\circ }\\ x& ={10}^{\circ }+k\cdot {120}^{\circ }\end{array}$
Untuk $k=0$, diperoleh $x={10}^{\circ }$.
Untuk $k=1$, diperoleh $x={130}^{\circ }$.
Untuk $k=2$, diperoleh $x={250}^{\circ }$.
Untuk $k=3$, diperoleh $x={370}^{\circ }$.
Kita tidak peroleh nilai $x$ yang memenuhi interval yang diberikan.
Kemungkinan 2
$\begin{array}{cc}3x& =(180-30{)}^{\circ }+k\cdot {360}^{\circ }\\ x& ={50}^{\circ }+k\cdot {120}^{\circ }\end{array}$
Untuk $k=0$, diperoleh $x={50}^{\circ }$.
Untuk $k=1$, diperoleh $x={170}^{\circ }$.
Untuk $k=2$, diperoleh $x={290}^{\circ }$.
Untuk $k=3$, diperoleh $x={410}^{\circ }$.
Kita peroleh hanya satu nilai $x$ yang memenuhi interval yang diberikan, yakni $x={290}^{\circ }$
(Jawaban C) 

[collapse]

Soal Nomor 14
Nilai maksimum dari $f\left(x\right)=\int (3\cos x-4\sin x)\text{d}x$ adalah $2$ kali nilai minimumnya. Nilai $f\left(0\right)=\cdots \cdot$
A. $12$                     C. $19$                    E. $25$
B. $15$                     D. $20$

Pembahasan

Pertama, integralkan dulu rumus fungsi $f$yang diberikan.
$$\begin{array}{cc}\int (3\cos x-4\sin x)\text{d}x& =3\sin x-4(-\cos x)+C\\ & =3\sin x+4\cos x+C\end{array}$$Bentuk $3\sin x+4\cos x$ dapat diubah menjadi $r\cos (x-p)$ dengan $r=\sqrt{4^2+3^2}=\sqrt{25}=5$. Nilai $p$ tidak perlu dicari.
Catatan: Bentuk $a\cos x+b\sin x$ sama dengan $r\cos (x-p)$ dengan $r=\sqrt{a^2+b^2}$dan $\tan p=\frac{b}{a}$, $-\pi \le p\le \pi$.
Kita peroleh, $f\left(x\right)=5\cos (x-p)+C$.
Nilai maksimum $f\left(x\right)$ tercapai saat $\cos (x-p)$ bernilai maksimum, yaitu $1$, sedangkan nilai minimumnya tercapai saat $\cos (x-p)$ bernilai minimum, yaitu $-1$.
Karena nilai maksimum dua kali nilai minimum $f\left(x\right)$, maka kita tulis
$$\begin{array}{cc}{f}_{\text{maks}}\left(x\right)& =2\left(f_{\text{min}}\right(x\left)\right)\\ 5\left(1\right)+C& =2\left(5\right(-1)+C)\\ 5+C& =-10+2C\\ C& =15\end{array}$$Jadi, rumus fungsi $f\left(x\right)=3\sin x+4\cos x+15$, sehingga 
$$\begin{array}{cc}f\left(0\right)& =3\sin 0+4\cos 0+15\\ & =3\left(0\right)+4\left(1\right)+15=19\end{array}$$(Jawaban C)

[collapse]

Bagian Uraian

Soal Nomor 1
Tentukan periode, nilai maksimum, dan nilai minimum fungsi trigonometri berikut.
a. $f\left(x\right)=2\sin 3x$
b. $f\left(x\right)=-3\cos 2x$
c. $f\left(x\right)=4\tan \frac{1}{3}x$

Pembahasan

Jawaban a)
Bentuk umum fungsi sinus tersebut adalah $f\left(x\right)=a\sin kx$.
Oleh karena fungsi $f\left(x\right)=2\sin 3x$, maka $a=2$ dan $k=3$.
1) Periode $=\frac{{360}^{\circ }}{k}=\frac{{360}^{\circ }}{3}={120}^{\circ }$
2) Nilai maksimum $=a=2$
3) Nilai minimum $=-a=-2$
Jawaban b)
Bentuk umum fungsi cosinus tersebut adalah $f\left(x\right)=a\cos kx$.
Oleh karena fungsi $f\left(x\right)=-3\cos 2x$, maka $a=-3$ dan $k=2$.
1) Periode $=\frac{{360}^{\circ }}{k}=\frac{{360}^{\circ }}{2}={180}^{\circ }$
2) Nilai maksimum $=-a=-(-3)=3$
3) Nilai minimum $=a=-3$
Jawaban c)
Bentuk umum fungsi tangen tersebut adalah $f\left(x\right)=a\tan kx$.
Oleh karena fungsi $f\left(x\right)=4\tan \frac{1}{3}x$, maka $a=4$ dan $k=\frac{1}{3}$.
1) Periode $=\frac{{180}^{\circ }}{k}=\frac{{360}^{\circ }}{\frac{1}{3}}={540}^{\circ }$
2) Nilai maksimum $\infty$
3) Nilai minimum $-\infty$
Catatan: fungsi tangen tidak memiliki amplitudo dan nilai maksimum/minimumnya tak hingga (atau negatif tak hingga). 

[collapse]

Soal Nomor 2
Tentukan fungsi yang sesuai dengan gambar grafik berikut.

Pembahasan

Jawaban a)
Perhatikan sketsa gambar berikut.

Apabila grafik di atas digeser ke arah kanan sehingga titik ujungnya di $(0,0)$, maka diperoleh grafik sinus berbentuk $f\left(x\right)=y=a\sin k(x-\theta )$. Diketahui bahwa nilai maksimum dan minimum fungsi pada grafik adalah $3\text{dan}-3$, sehingga 
$\begin{array}{cc}a& =\frac{\text{N. Maksimum}-\text{N. Minimum}}{2}\\ & =\frac{3–(-3)}{2}=3\end{array}$
Tampak juga bahwa periode grafiknya adalah $2\pi ={360}^{\circ }$, sehingga
$k=\frac{2\pi }{\text{Periode}}=\frac{2\pi }{2\pi }=1$
Karena pergeserannya ke arah kanan sebesar $\frac{\pi }{4}$, maka $\theta =-\frac{\pi }{4}$ (bertanda negatif bila digeser ke kanan), sehingga rumus fungsinya adalah $f\left(x\right)=3\sin (x+\frac{\pi }{4})$
Jawaban b) 
Perhatikan sketsa gambar berikut.

Apabila grafik di atas digeser ke arah kanan sehingga titik ujungnya di $(0,0)$, maka diperoleh grafik sinus berbentuk $f\left(x\right)=y=a\sin k(x-\theta )$. Diketahui bahwa nilai maksimum dan minimum fungsi pada grafik adalah $1\text{dan}-1$, sehingga 
$\begin{array}{cc}a& =\frac{\text{N. Maksimum}-\text{N. Minimum}}{2}\\ & =\frac{1–(-1)}{2}=1\end{array}$
Tampak juga bahwa periode grafiknya adalah ${180}^{\circ }$, sehingga
$k=\frac{{360}^{\circ }}{{180}^{\circ }}=2$
Karena pergeserannya ke arah kanan sebesar ${30}^{\circ }$, maka $\theta =-{30}^{\circ }$ (bertanda negatif bila digeser ke kanan), sehingga rumus fungsinya adalah $f\left(x\right)=\sin 2(x+{30}^{\circ })$. 

[collapse]